Paraang Euler

Sa matematika at komputasyonal na agham, ang paraang Euler ay isang unang-order na paraang numerikal para sa paglutas ng mga ekwasyong ordinaryong diperensiyal(ODE) na may isang ibinigay na inisyal na halaga. Ito ang pinaka basikong paraang hayagan para sa numerikal na integrasyon ng mga ekwasyong ordinaryong diperensiyal at ang pinaka simpleng paraang Runge-Kutta. Ang paraang Euler ay ipinagangalan kay Leonard Euler na trumato nito sa kanyang aklat na Institutionum calculi integralis (na inilimbag noong 1768–70). Ang paraang Euler ay isang paraang unang order na nangangahulugan ang lokal na pagkakamali(pagkakamali kada hakbang) ay proporsiyonal sa kwadrado ng sukat ng hakbang at ang pagkakamaling global(pagkakamali sa isang ibinigay na panahon) ay proporsiyonal na sukat ng hakbang. Ito ay dumaranas rin mula sa mga problemang pagiging matatag. Para sa mga dahilang ito, ang paraang Euler ay hindi kadalasang ginagamit sa pagsasanay. Ito ay nagsisilbing basehan upang lumikha ng mas komplikadong mga paraan.

Ilustrayon ng paraang Euler. Ang hindi alam na kurba ay nasa asul at ang aproksimasyong poligonal nito ay nasa pula.

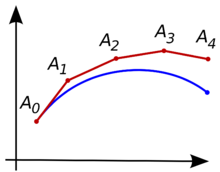
Inpormal na paglalarawang heometrikal

Isaalang alang ang problema ng pagkukwenta ng hugis ng isang hindi alam na kurba na nagsisimula sa isang ibinigay na punto at sumasapat sa isang ibinigay na ekwasyong diperensiyal. Dito, ang isang ekwasyong diperensiyal ay maaaring akalain bilang isang pormula kung saan ang lihis ng linyang tangent sa kurba ay maaaring kwentahin sa anumang punto sa kurba kapag ang posisyon ng puntong ito ay nakwenta na. Ang ideya ay bagaman ang kurba ay hindi alam sa simula, ang pasimulang punto nito na ating tutukuying $A_{0},$ ay alam. Pagkatapos, mula sa ekwasyong diperensiyal, ang lihis sa kurba sa $A_{0}$ ay maaaring kwentahin at kaya ang linyang tangent. Kumuha ng isang maliit na hakbang sa kahabaan ng linyang tangent hanggang sa isang puntong $A_{1}.$ Sa kahabaan ng maliit na hakbang na ito, ang lihis ay hindi labis na nagbabago kaya ang $A_{1}$ ay magiging malapit sa kurba. Kung tayo'y magpapanggap na ang $A_{1}$ ay nasa kurba pa rin, ang parehong pangangatwiran gaya ng sa puntong $A_{0}$ sa itaas ay maaring gamitin. Pagkatapos ng ilang mga hakbang, ang isang kurbang poligonal na $A_{0}A_{1}A_{2}A_{3}\dots$ ay kukwentahin. Sa pangkalahatan, ang kurbang ito ay hindi lumilihis ng labis na malayo mula sa orihinal na hindi alam na kurba at ang pagkakamali sa pagitan ng dalawang mga kurba ay maaaring gawing maliit kung ang sukat ay sapat na maliit ang ang interbal ng komputasyon ay may hangganan.

Pormulasyon ng paraan

Ipagpalagay na nais nating tantiyahin ang solusyo ng problemang inisyal na halaga na

$y'(t)=f(t,y(t)),\qquad \qquad y(t_{0})=y_{0}.$

Pumili ng isang halagang $h$ para sa sukat ng bawat hakbang at itakda ang $t_{n}=t_{0}+nh$. Ngayon, ang isang hakaban ng paraang Euler mula sa $t_{n}$ to $t_{n+1}=t_{n}+h$ ay

$y_{n+1}=y_{n}+hf(t_{n},y_{n}).\qquad \qquad$

ng halaga ng $y_{n}$ ay isang aproksimasyon ng solusyon sa ODE sa panahong $t_{n}$: $y_{n}\approx y(t_{n})$. Ang paraang Euler ay hayagan, i.e. ang solusyong $y_{n+1}$ ay isang hayagang punsiyon ng $y_{i}$ for $i\leq n$.

Bagaman ang paraang Euler ay nag-iintegrado ng isang unang order na ODE, ang anumang ODE ng order na N ay maaaring ikatawan bilang isang unang order na ODE: upang tratuhin ang ekwasyong

$y^{(N)}(t)=f(t,y(t),y'(t),\ldots ,y^{(N-1)}(t))$,

ating ipakikilala ang mga sumusuportang baribulong $z_{1}(t)=y(t),z_{2}(t)=y'(t),\ldots ,z_{N}(t)=y^{(N-1)}(t)$ at makamit ang katumbas na ekwasyong

$\mathbf {z} '(t)={\begin{pmatrix}z_{1}'(t)\\\vdots \\z_{N-1}'(t)\\z_{N}'(t)\end{pmatrix}}={\begin{pmatrix}y'(t)\\\vdots \\y^{(N-1)}(t)\\y^{(N)}(t)\end{pmatrix}}={\begin{pmatrix}z_{2}(t)\\\vdots \\z_{N}(t)\\f(t,z_{1}(t),\ldots ,z_{N}(t))\end{pmatrix}}$

Ito ang isang sistemang unang order sa bariabulong $\mathbf {z} (t)$ at maaaring hawakan ng paraang Euler o sa katotohanan ng anumang ibang skema para sa mga sistemang unang order.

Halimbawa

Sa ibinigay na problemang inisyal na halagang

$y'=y,\quad y(0)=1,$

nais nating gamitin ang paraang Euler upang tantiyahin ang $y(4)$.

Paggamit ng sukat ng hakbang na katumbas ng 1

Ilutrasyon ng integrasyong numerikal para sa ekwasyong $y'=y,y(0)=1.$ Ang asul ang paraang Euler, ang berde ang paraaang gitnang punto, ang pula ang eksaktong solusyong $y=e^{t}.$ Ang sukat ng hakbang ay h = 1.0.

Ang paraang Euler ay

$y_{n+1}=y_{n}+hf(t_{n},y_{n}).\qquad \qquad$

kaya dapat nating kwentahin ang $f(t_{0},y_{0})$. Sa simpleng ekwasyong diperensiyal na ito, ang punsiyong $f$ ay inilalarawan ng $f(t,y)=y$. Mayroon tayong

$f(t_{0},y_{0})=f(0,1)=1.\qquad \qquad$

Sa paggawa ng hakbang sa itaas, ating natagpuan ang lihis ng linya na tangent sa kurbang solusyon sa puntong $(0,1)$. Tandaan na ang lihis ay inilalarawan bilang pagbabago sa $y$ na hinati ng pagbabago sa $t$, o $\Delta y/\Delta t$.

Ang susunod na hakban ay paramihin ang halaga sa itaas sa sukat ng hakbang na $h$ na ating kukuning katumbas sa isang narito:

$h\cdot f(y_{0})=1\cdot 1=1.\qquad \qquad$

Dahil ang sukat ng hakbang ang pagbabago sa $t$, kung ating pararamihin ang sukat ng hakban at ang lihis ng tangent, ating makukuha ang pagbabago sa halagang $y$ value. Ang halagang ito ay idadagdag naman sa inisyal na halagang $y$ upang makamit ang susunod na halagang gagamit para sa mga pagkukwenta.

$y_{0}+hf(y_{0})=y_{1}=1+1\cdot 1=2.\qquad \qquad$

Ang mga hakbang sa itaas ay dapt ulitin upang mahanap ang $y_{2}$, $y_{3}$ at $y_{4}$.

${\begin{aligned}y_{2}&=y_{1}+hf(y_{1})=2+1\cdot 2=4,\\y_{3}&=y_{2}+hf(y_{2})=4+1\cdot 4=8,\\y_{4}&=y_{3}+hf(y_{3})=8+1\cdot 8=16.\end{aligned}}$

Dahil sa paulit ulit na kalikasan ng algoritmong ito, makakatulong na ayusin ang mga pagkukwenta sa isang anyong tsart gaya ng makikita sa ibaba upang maiwasan ang paggawa ng mga pagkakamali.

$n$	$y_{n}$	$t_{n}$	$f(t_{n},y_{n})$	$h$	$\Delta y$	$y_{n+1}$
0	1	0	1	1	1	2
1	2	1	2	1	2	4
2	4	2	4	1	4	8
3	8	3	8	1	8	16

Ang konklusyon ng pagkukwentang ito ang $y_{4}=16$. Ang eksaktong solusyon ng ekwasyong diperensiyal ay $y(t)=e^{t}$ kaya ang $y(4)=e^{4}\approx 54.598$. Kaya ang aproksimasyon ng paraang Euler ay hindi napaka buti sa kasong ito. Gayunpaman, gaya ng ipinapakita ng pigura, ang pag-aasal nito ay kwalitatibong tama.

Paggamit ng ibang mga sukat ng hakbang

Ang parehong ilustrasyon para sa h = 0.25.

Gaya ng iminungkahi sa introduksiyon, ang paraang Euler ay mas tiyak kung ang mga sukat ng hakbang na $h$ ay mas maliit. Ang tabla sa ibaba ay nagpapakita ng resultang may iba't ibang mga sukat ng hakbang. Ang taas na row ay tumutugon sa halimbawa ng nakaraang seksiyon at ang ikalawang row ay ipinapakita sa pigura.

sukat ng hakbang	resulta ng paraang Euler	pagkakamali
1	16	38.598
0.25	35.53	19.07
0.1	45.26	9.34
0.05	49.56	5.04
0.025	51.98	2.62
0.0125	53.26	1.34

Ang itinalang pagkakamali sa huling column ng tabla ang pagkakaiba sa pagitan ng eksaktong solusyon sa $t=4$ at ang aproksimasyong Euler. Sa ilalim ng tabla, ang sukat ng hakban ay kalahati ng sukat ng hakban sa nakaraang row at ang pagkakamali ay tinatayang kalahati rin ng pagkakamali ng nakaraang row. Ito ay nagmumungkahing ang pagkakamali ay mga proporsiyonal sa sukat ng hakban, kahit papano para sa katamtamang maliit na mga halaga ng sukat ng hakbang. Ito ay totoo sa pangkalahatanat para sa ibang mga ekwasyon. Ang ibang mga paraan gaya ng paraang gitnang punto na ipinapakita rin sa mga pigura ay umaasal ng mas mapapaboran. Ang pagkakamali ng paraang gitnang punto ay mga proporsional sa kwadrado ng bawat sukat ng hakbang. Dahil dito, ang paraang Euler ay sinasabing isang paraang unang order samantalang ang paraang gitnang punto ay ikalawang order. Pwede nating iekstrapola mula sa taas na tabla na ang bawat sukat ng hakban na kailangan upang makuha ang sagot na tama sa mga lugar na tatlong desimal ay tinatayang 0.00001 na ngangahulugan kailangan nating mga 400,000 hakbang. Ang malaking bilang na ito ng mga hakbang ay nag aatas ng isang mataas na gastos na komputasyon. Dahil dito, ang mga tao ay karaniwang gumagamit ng alternatibong mga paraang mataaas na order gaya ng mga paraang Runge-Kutta o mga paraang linyar maraming hakbang lalo na kung ang isang mataas na pagiging tumpak ay ninanais.

Mga sanggunian

• Atkinson, Kendall A. (1989), An Introduction to Numerical Analysis (ika-2nd (na) edisyon), New York: John Wiley & Sons, ISBN 978-0-471-50023-0{{citation}}: CS1 maint: date auto-translated (link).
• Ascher, Uri M.; Petzold, Linda R. (1998), Computer Methods for Ordinary Differential Equations and Differential-Algebraic Equations, Philadelphia: Society for Industrial and Applied Mathematics, ISBN 978-0-89871-412-8{{citation}}: CS1 maint: date auto-translated (link).
• Butcher, John C. (2003), Numerical Methods for Ordinary Differential Equations, New York: John Wiley & Sons, ISBN 978-0-471-96758-3{{citation}}: CS1 maint: date auto-translated (link).
• Hairer, Ernst; Nørsett, Syvert Paul; Wanner, Gerhard (1993), Solving ordinary differential equations I: Nonstiff problems, Berlin, New York: Springer-Verlag, ISBN 978-3-540-56670-0{{citation}}: CS1 maint: date auto-translated (link).
• Iserles, Arieh (1996), A First Course in the Numerical Analysis of Differential Equations, Cambridge University Press, ISBN 978-0-521-55655-2{{citation}}: CS1 maint: date auto-translated (link)
• Stoer, Josef; Bulirsch, Roland (2002), Introduction to Numerical Analysis (ika-3rd (na) edisyon), Berlin, New York: Springer-Verlag, ISBN 978-0-387-95452-3{{citation}}: CS1 maint: date auto-translated (link).
• Lakoba, Taras I. (2012), Simple Euler method and its modifications (PDF) (Lecture notes for MATH334, University of Vermont), inarkibo mula sa orihinal (PDF) noong 12 Hulyo 2012, nakuha noong 29 Pebrero 2012{{citation}}: CS1 maint: date auto-translated (link).