Teorya ng kontrol

Ang Teoriya ng kontrol o teoriya ng taban (Ingles: Control theory) ay isang interdisiplinaryong sangay ng inhinyerya at matematika na umuukol sa pag-aasal ng mga sistemang dinamikal na may mga pagpapasok o input (paglalagay na papaloob). Ang panglabas na input ng isang sistema ay tinatawag na reperensiya. Kapag ang isa o maraming mga bariabulong awtput ng isang sistema ay kailangan upang sumunod sa isang reperensiya sa loob ng isang panahon, ang kontroler ay nagmamanipula ng mga input sa isang sistema upang makamit ang ninanais na epekto sa awtput ng sistema. Ang karaniwang layunin ng isang teoriya ng kontrol ang pagkukwenta ng mga solusyon para sa angkop nagtutuwid na aksiyon mula sa kontroler na nagreresulta sa pagiging matatag ng sistema na nangangahulugan ang sitema ay hahawak ng hanay ng punto at hindi umugoy sa palibot nito. Ang mga input at awtput ng isang tuloy tuloy na sistemang kontrol ay pangkalahatang nauugnay sa mga ekwasyong diperensiyal. Kung ang mga ito ay linyar na konstanteng mga koepisyente, ang isang punsiyong paglilipat na nuugnay sa input at awtputay maaaring makamit sa pamamagitan ng pagkuha ng transpormang Laplace ng mga ito. Kung ang mga ekwasyong diperensiyal ay hinid linyar at may isang alam na solusyon, maaaaring posibleng ilinyar ang mga ekwasyong diperensiyal na hindi linyar sa solusyong ito.^[1] Kung ang nagreresultang mga ekwasyong diperensiyal na linyar ay mga konstanteng koepisyente, maaaring kunin ng isa ang mga transpormang Laplace nito upang makamit ang punsiyong paglilipat. Ang punsiyong paglilipat ay kilala rin bilang punsiyon ng sistema o punsiyong network. Ang punsiyong paglilipat ay isang matematikal na representasyon sa mga termino ng prekwensiyang pang-espasyo o temporal ng relasyon sa pagitan ng input at awtput ng isang solusyong linyar na hindi nababago ng panahon ng mga ekwasyong diperensiyal na hindi linyar na naglalarawan sa sistema. Ang malawak na paggamit ay karaniwang gawa sa isang istilong diagramatiko na tinaguriang diagramang bloke.

Buod

Ang teoriya ng kontrol ay

isang teoriya na umuukol sa pag-iimpluwensiya ng pag-aasal ng mga sistemang dinamikal
isang interdisiplinaryong pang-ilalim na larangan ng agham na nagmumula sa inhinyerya at matematika at nag-ebolb sa paggamit ng mga agham panlipunan tulad ng sikolohiya, sosyolohiya, kriminolohiya at sa sistemang pinansiyal.

Ang mga sistemang kontrol ay maaaring isipin na mayroong apat na mga tungkulin: pagsukat, paghahambing, pagkukwenta at pagtutuwid. Ang mga apat na tungkuling ito ay kinukumpleto ng limang mga elemento: detektor, tranduser, transmitter, kontroler at ang huling elementong kontrol. Ang punsiyong pagsukat ay kinukumpleto ng detektor, transduser at transmitter. Sa mga praktikal na aplikasyon, ang tatlong mga elementong ito ay karaniwang nilalaman sa isang unit. Ang isang pamantayang halimbawa ang termometer ng resitansiya. Ang mga punsiyong paghahambing at pagkukwenta ay kinukumpleto sa looob ng kontroler na maaaring makumpleto ng elektroniko sa pamamagitan ng isang proporsiyonal na kontrol, kontroler na PI, kontroler na PID, bistable, kontrol na histeretiko o kontroler na mapopogramang lohika. Ang tamang punsiyon ay kinukumpleto ng isang huling elementong kontrol. Ang huling elementong kontrol ay nagbabago ng input o awtput sa sistemang kontrol na umaapekto sa minanipula o kinontrol na bariabulo.

Isang halimbawa

Isaalang ang kontrol na paglalayag (engl.cruise control) ng isang kotse na isang kasangkapang nilikha upang panatilihin ang bilis ng sasakyan sa isang konstanteng ninanais o reperensiyang bilis na ibinigay ng tsuper. Ang kontroler ang kontrol na cruise, ang planta ang kotse at ang sistema ang kotse at ang kontrol na cruise. Ang awtput ng sistema ang bilis ng kotse at ang mismong kontrol ang posisyong trotelya (engl.throttle) ng makina na tumutukoy kung gaanong kapangyarihan ang nalilikha. Ang isang primitibong paraan upang ipatupad ang kontrol ay simpleng ikandado ang posisyong trotelya kapag ang tsuper ay nagsasagawa ng kontrol na cruise. Gayunpaman, kung ang kontrol na cruise lumalahok sa isang tuluy-tuloy na patag na kalye, kung gayon ang kotse ay maglalakbay ng mas mabagal papaakyat at mas mabilis pababa. Ang uring ito ng kontroler ay tinatawag na kontroler na bukas na loop dahil ang pagsukat ng awtput ng sistema(ang bilis ng kotse) ay ginagamit upang baguhin ang kontrol(posisyong trotelya). Bilang resulta, ang kontrol ay hindi makagpupuno para sa mga pagbabagong umaasal sa kotse tulad ng isang pagbabago sa lihis ng kalye. Ang isang sistemang kontrol na saradong-loop ay isang sensor na nagmomonitor ng awtput ng sistema(bilis ng kotse) at nagpapasok ng mga datos sa isang kontroler na nagsasaayod ng kontrol(posisyon ng trotelya) kung kinakailangan upang panatiliin ang ninanais na ouput ng sistema(itugma ang bilis ng kotse sa reperensiyang bilis). Ngayon, kung ang kotse ay umakyat, ang pagbabawas sa bilis ay sinusukat at ang posisyong trotelya ay babaguhin upang pataasin ang kapangyarihan ng makina na nagpapabilis sa sasakyan. Ang feedback mula sa pagsukat ng bilis ng kotse ay pumapayag sa kontrol na dinamikong magpuno ng mga pagbabago sa bilis ng kotse. Mula sa feedback na ito na ang paradaym ng kontrol loop ay lumilitaw: ang kontrol ay umaapekto sa awtput ng sistema na sumusukat naman at nagloloop pabalik upang baguhin ang kontrol.

Klasikong teoriya ng kontrol

Upang mapaglabanan ang mga limitasyon ng kontrol na bukas na loop, ang teoriya ng kontrol ay nagpapakilala ng reaksiyon (engl.feedback). Ang isang kontroler na saradong-loop ay gumagamit ng feedback upang kontrolin ang mga estado o mga ouput ng isang sistemang dinamikal. Ang pangalan nito ay nagmumula mula sa landas ng impormasyon sa sistema: ang mga input ng proseso(e.g. boltaheng nilapat sa motor na elektriko) ay may epekto sa mga awtput ng proseso(e.g. bilis o torke ng motor) na nasusukat ng mga sensor at pinoproseso ng kontroler. Ang resulta(signal ng kontrol) ay ginagamit bilang input ng proseso ng nagsasara ng loop.

Ang mga kontroler na saradong-loop ay may sumusunod na mga pakinabang sa mga kontroler na bukas na loop:

pagtatakwil ng kaabalahan(gaya ng mga bundok sa kontrol ng cruise sa itaas)
na-garantiyang pagganap kahit sa mga kawalang katiyakang modelo kapag ang istraktura ng modelo ay hindi perpektong tumutugma sa tunay na proseso at ang mga parametro ng modelo ay hindi eksakto
ang mga hindi matatag na proseso ay mapapatatag
lumiit na sensitibo sa mga pagkakaiba ng parametro
napabuting pagganap ng pagsubaybay ng reperensiya

Sa ilang mga sistema, ang kontrol na loop na sarado at bukas na loop ay ginagamit ng sabay. Sa gayong mga sistema, ang kontrol na bukas na loop ay tinaguriang feedforward at nagsisilbi na karagdagang magpabuti ng pagganap ng pagsubaybay ng reperenisya. Ang isang karaniwang arkitektura ng kontroler na saradong loop ang kontroler na PID

Punsiyong paglipat na saradong loop

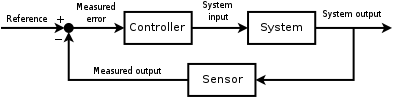
Ang awtput ng sistemang y(t) ay pinapakain ng pabalik sa pamamagitan ng pagsukat ng isang sensor na F sa halagang reperensiyang r(t). Ang kontroler na C ay kumukuha naman ng pagkakamaling e (pagkakaiba) sa pagitan ng reperensiya at awtput sa pababago sa mga input na u sa sistema sa ilalim ng kontrol na P. Ito ay pinapakita sa larawan. Ang uring ito ng kontroler ay isang saradong loop o kontroler na feedback. Ito ay tinatawag na isang isang-input-isang-ouput (SISO) na sistemang kontrol. Ang mga sistemang MIMO (i.e., Multi-Input-Multi-awtput) na may higit sa isang input/awtput ay karaniwan. Sa gayong mga kaso, ang mga bariabulo ay kinakatawan sa pamamagitan ng mga bektor kesa sa simpleng mga halagang skalar. Para sa isang mga sistemang inpinamahaging parametro, ang mga bektor ay maaaring walang hangganang dimensiyonal(na karaniwang mga punsiyon).

Isang simpleng feedback control loop

Kung ating ipagpapalagay na ang kontroler C, ang plantang P at ang sensor na F ay linyar at hindi nababago ng panahon(i.e. ang mga elemento ng kanilang punsiyong paglilipat na 'C(s), P(s), at F(s) ay hindi nakasalalay sa panahon), ang mga sistema sa itaaas ay maaaring suriin gamit ang transpormang Laplace sa mga bariabulo. Ito ay nagbibigay ng mga sumusunod na relasyon:

Y(s)=P(s)U(s)\,\!

U(s)=C(s)E(s)\,\!

E(s)=R(s)-F(s)Y(s).\,\!

Ang paglutas ng Y(s) sa mga termino ng R(s) ay nagbibigay ng:

Y(s)=\left({\frac {P(s)C(s)}{1+F(s)P(s)C(s)}}\right)R(s)=H(s)R(s).

Ang ekspresyong $H(s)={\frac {P(s)C(s)}{1+F(s)P(s)C(s)}}$ ay tinutukoy na punsiyong paglilipat sa saradong loop ng sistema. Ang numerador ang pasulong(bukas na loop) na pakinabang mula r tungo sa y at ang denominador ay isa na dinagdagan ng pakinabang sa paglalakbay sa feedback loop na tinatwag na pakinabang na loop. Kung ang $|P(s)C(s)|\gg 1$ , i.e., ito ay may isang malaking norma sa bawat halaga ng s at kung ang $|F(s)|\approx 1$ , kung gayon, angY(s) ay tinatayang katumbas ng R(s) at ang awtput ay malapit na sumusubaybay sa reperensiyang input.

Kontroler na PID

Para sa mas marami pang mga detalye hinggil sa paksang ito, tingnan ang Kontroler na PID.

Ang kontroler na PID ay malamang na pinaka-ginagamit na disenyong kontrol na feedback. Ang PID ang akronimo para sa Proportional-Integral-Derivative na tumutukoy sa tatlong mga termino na gumagana sa pagkakamaling signal upang lumikha ng isang kontrol na signal. Kung ang u(t) ang kontrol na signal na ipinadala sa sistema, ang y(t) ang sinukat na awtput at ang r(t) ang ninanais na awtput, at ang pagkakamaling pagsubaybay na $e(t)=r(t)-y(t)$ na isang kontroler na PID ay may pangkalahatang anyong

u(t)=K_{P}e(t)+K_{I}\int e(t){\text{d}}t+K_{D}{\frac {\text{d}}{{\text{d}}t}}e(t).

Ang ninanais na dinamikang saradong loop ay makakamit sa pamamagitan ng pagsasaayos ng tatlong mga parametrong $K_{P}$ , $K_{I}$ at $K_{D}$ na kadalasang paulit ulit sa pamamagitan ng pagtotono at ng walang spesipikong kaalaman ng modelong planta. Ang pagiging matatag ay kadalasang nasisiguro sa pamamagitan lamang ng proporsiyonal na termino. Ang integral ay pumapayag sa pagtatakwil ng pagkaabala ng hakbang. Ang terminong deribatibo ay ginagamit upang magbigay ng pagbabawas o paghuhugis ng tugon. Ang mga kontroler na PID ang pinaka-mahusay na nalikhang klase ng mga sistemang kontrol. Gayunpaman, ang mga ito ay hindi maaaring gamitin sa ilang mga mas komplikadong kaso lalo na kung ang mga sistemang MIMO ay isinasaalang alang.

Ang paglalapat ng transpormasyong Laplace ay nagreresulta sa natranspormang ekwasyong kontroler na PID

u(s)=K_{P}e(s)+K_{I}{\frac {1}{s}}e(s)+K_{D}se(s)

u(s)=(K_{P}+K_{I}{\frac {1}{s}}+K_{D}s)e(s)

sa punsiyong paglilipat na kontroler na PIC

C(s)=(K_{P}+K_{I}{\frac {1}{s}}+K_{D}s).

Modernong teoriya ng kontrol

Salungat sa analisis ng sakop na prekwensiya ng klasikong teoriya ng kontrol, ang modernong teoriya ng kontrol ay gumagamit ng sakop-panahong estadong espasyong representasyon na isang modelong matematikal ng isang sistemang pisikal bilang isang hanay ng input, awtput at mga bariabulo ng estado na nuugnay sa unang order na mga ekwasyong diperensiyal. Upang iabstrakto mula sa bilang ng mga input, mga awtput at mga estado, ang mga bariabulo ay inihahayag bilang mga bektor at ang mga ekwasyong diperensiyal at alhebraiko ay isinusulat sa anyong matriks(ang huli ay tanging posible kapag ang sistemang dinamikal ay linyar). Ang estadong espasyong representasyon(na kilala rin bilang "pakikitungong sakop-panahon") ay nagbibigay ng maginhawa at siksik na paraan upang imodelo at suriin ang mga sistema na may maraming mga input at awtput. Hindi tulad ng pakikitungong sakop na prekwensiya, ang paggamit ng representasyong estadong espasyo ay hindi limitado sa mga sistemang may mga bahaging linyar at mga kondisyong inisyal na sero. Ang espasyong estado ay tumutukoy sa espasyong ang mga aksis ang mga bariabulo ng estado. Ang estado ng sistema ay maaaring ikatawan bilang isang bektor sa loob ng espasyong ito. ^[2]

Mga paksa sa teoriya ng kontrol

Pagiging matatag

Ang pagiging matatag ng isang pangkalahatang sistemang dinamika na walang input ay maaaring ilarawan ng kriteryang pagiging matatag na Lyapunov. Ang isang sistemang linyar na kumukuha ng input ay tinatawag na punsiyong BIBO kung ang awtput nito ay mananatili tinakdaan para sa anumang tinakdaang input. Ang pagiging matatag para sa sistemang hindi linyar na kumukuha ng input ay pagiging matatag na input tungo sa estado(ISS) na nagsasama ng pagiging matatag na Lyapuno at isang katulad na nosyon sa pagiging matatag na BIBO. Para sa simplisidad, ang sumusunod na mga paglalarawan ay pumopokus sa mga sistemang linyar na tuloy tuloy sa panahon at diskreto sa panahon. Sa matematikal na paglalarawan, ito ay nangangahulugang para sa isang kaswal na sistemang linyar na magiging matatag, ang lahat ng mga polo ng punsiyong paglilipat nito ay dapat mayroong negatibong mga real na bilang, i.e. ang real na bahagi ng lahat ng mga polo ay mababa sa sero. Sa pagsasalitang praktikal, ang pagiging matatag ay nag-aatas na ang punsiyong paglilipat na mga polong kompleks ay tumatahan

sa bukas na kaliwang kalahati ng planong kompleks para sa tuluy-tuloy na panahon kapag ang transpormang Laplace ay ginagamit upang makamit ang punsiyong paglilipat.
sa loob ng bilog na unit para sa diskretong panahon kapag ang transpormang-Z ay ginagamit.

Ang pagkakaiba sa pagitan ng dalawang mga kaso ay simpleng sanhi ng paraang tradisyonal ng pagbakas ng panahong tuloy tuloy laban sa mga punsiyon paglipat na panahong diskreto. Ang tuloy tuloy na transpormang Laplace sa mga koordinatong Cartesian kung saan ang $x$ na aksis ang real na aksis at ang diskretong transpormang-Z ay nasa mga koordinatong sirkular kung ang $rho$ aksis ang real na aksis. Kapag ang angkop na mga kondisyon sa itaas ay nasapatan, ang isang sistema ay sinasabing asimptotikong matatag: ang mga bariabulo ng isang asimptotikong matatag na sistemang kontrol ay palaging nababawasan mula sa insiyal na halaga ng mga ito at hindi nagpapakita ng permanenteng mga osilasyon. Ang mga permanenteng osilasyon ay nangyayari kapag ang polo ay may isang real na bahagi na eksaktong katumbas ng sero(sa kasong panahong tuloy tuloy) o katumbas na modulus sa isa(sa kaso ng panahong diskreto). Kung ang isang simpleng tugon ng matatag na sistema ay hindi nabubulok o lumalago sa paglipas ng panahon at walang mga osilasyon, ito ay [[marhinal na pagiging matatag|marhinal na matatag: sa kasong ito, ang punsiyong pagliipat ng sistema ay walang hindi umuulit na mga polo sa origin ng planong kompleks(i.e. ang bahaging real at kompleks ng mga ito ay sero sa kasong panahong tuloy tuloy). Ang mga osilasyon ay umiiral kapag ang mga polong may real na bahagi na katumbas ng sero ay may bahaging imahinaryo na hindi katumbas ng sero. Kung ang sistemang isinasaalang alang ay may tugong impulse ng

\ x[n]=0.5^{n}u[n]

kung gayon, ang transpormang-Z ay ibinigay ng

\ X(z)={\frac {1}{1-0.5z^{-1}}}\

na may polo sa $z=0.5$ (serong imahinaryong bahagi). ANg sistemang ito ay matatag na BIBO(na asimptotiko) dahil ang polo ay nasa loob ng bilog na unit. Gayunpaman, kung ang tugong impulse ay

\ x[n]=1.5^{n}u[n]

kung gayon, ang transpormang-Z ay

\ X(z)={\frac {1}{1-1.5z^{-1}}}\

na may polo sa $z=1.5$ at hindi matatag na BIBO dahil ang polus ay striktong modulus na mas malaki sa isa. Ang maraming mga kasangkapan ay umiiral para sa analisis ng mga polo ng isang sistema. Ang mga ito ay kinabibilangan ng mga grapikal na sistemang tulad ng ugat na locus, mga pagbabakas na Bode at mga pagbabakas na Nyquist. Ang mga pagbabagong mekanikal ay maaaring gumawa sa kasapan at mga sistemang kontrol na mas matatag. Ang mga mandaragat ay nagdaragdag ng ballast upang pabutihin ang pagiging matatag ng mga barko. Ang mga barkong cruise ay gumagamit ng mga antiroll fin na lumalawig na nakahalang mula sa gilid ng barka na marahil ay 30 talampakan at tuloy tuloy na umiikot sa kanilang mga aksis upang bumuo ng mga pwersa na sumasalungat sa roll.

Pagiging makokontrol at pagiging mapagmamasdan

Ang pagiging makokontrol at pagiging mapagmamasdan ang pangunahing mga isyu sa analisis ng isang sistema bago pagpasyahan ang pinakamahusay na stratehiyang kontrol na ilalapat o kung kahit posibleng makontrol o mapatatag ang sistema. Ang pagiging makokontrol ay kaugnay ng posibilidd ng pagpupwera ng sistema sa isang partikular na estado sa pamamagitan ng paggamit ang angkop ng signal na kontrol. Kung ang isang estado ay hindi makokontrol, kung gayon, walang signal ang kailanman makakokontrol sa estado. Kung ang estado ay hindi makokontrol ngunit ang mga dinamika nito ay matatag, kung gayon ang estado ay tinaguriang mapapatatag. Ang pagiging mapagmamasdan bagkus ay kaugnay na posiblidad ng pagmamasid sa pamamagitan mga sukat na awtput na estado ng sistema. Kung ang isang estado ay hindi mapagmamasdan, ang kontrol ay hindi kailanman makakatukoy ng pag-aasal ng hindi mapagmamasdang estado at kaya ay hindi ito magagamit upang patatagin ang sistema. Gayunpaman, katulad ng kondisyong pagiging matatag sa itaas, kung ang estdo ay hindi makapagmamasid, ito ay maaari pa ring madedetekta. Mula sa pananaw na heometrikal, ang pagtingin sa mga estado ng bawat bariabulo ng sistema na kokontrolin, ang bawat masamang estado ng mga bariabulong ito ay dapat makokontrol at mapagmamasdan upang masiguro ang isang mabuting pag-aasal sa sistemang saradong loop. Ang ibig sabihin ay kung ang mga iginhalaga (eigenvalues) ng sistema ay hindi parehong makokontrol at mapagmamasdan, ang bahaging ito ng mga dinamika ay mananatiling hindi mahahawakan sa sistemang saradong loop. Kung ang gayong eigenhalaga ay hindi matatag, ang dinamika ng eigenhalagang ito ay iiral sa sistemang saradong look na kaya ay magiging hindi matatag. Ang mga hindi mapagmamasdang polo ay hindi umiiral sa realisasyon ng punsiyong paglilipat ng isang representasyong estado-espasyo na kaya minsan, ang huli ay ninanais sa analisis ng mga sistemang dinamikal. Ang mga solusyon sa problema ng sistemang hindi makokontrol at hindi mapagmamasdan ay kinabibilangan ng pagdaragdag ng mga aktuwator at mga sensor.

Spesipikasyon ng kontrol

Ang ilang mga iba't ibang stratehiyang kontrol ay nilikha sa mga nakaraang taon. Ang mga ito ay nagiiba iba mula sa sukdulang pangkalahatan(kontroler na PID) hanggang sa ibang mga nakatuon sa napaka partikular na mga klase ng mga sistema(lalo na ang robotika o kontrol na cruis ng sasakyang panghimpapawid). Ang isang problemang kontrol ay maaaring may ilang mga spesipikasyon. Ang pagiging matatag ay siyempre palaging umiiral: ang kontrol ay dapat sumiguro na ang sistemang saradong loop ay matatag kahit hindi isasaalang alang ang pagiging matatag ng bukas na loop. Ang isang mababang pagpipilian ng kontrol ay magpapasama sa pagiging matatag ng sistemang bukas na loop na dapat ay normal na iwasan. Minsan, ninanais na magkamit ng partikular na dinamika sa saradong loop: i.e. ang mga polo ay may $Re[\lambda ]<-{\overline {\lambda }}$ , kung saan ang ${\overline {\lambda }}$ ay isang nakapirmeng halaga na striktong mas malaki sa sero imbis na simpleng paghingi na ang $Re[\lambda ]<0$ . Ang isa pang karaniwang spesipikasyon ang pagtatakwil ng mga pagkaabala ng hakbang. Ang pagsasama ng integrador sa kadenang bukas na loop(i.e. nang direkta bago ang sistemang nasa ilalim ng kontrol) ay madalaing makapagkamit nito. Ang ibang mga klase ng pagkaabala ay nangangailangang isama ang iba't ibang mga uri ng pang-ilalim na sistema. Ang ibang mga spesipikasyon ng klasikong teoriya ng kontrol ay nagsasaalang alang sa tugong panahon ng sistemang saradong loop. Ito ay kinabibilangan ng panahong pagahon(ang panahong kailangan ng sistemang kontrol upang maabot ang ninanais na halaga pagkatapos ng perturbasyon), tuktok na overshoot(ang pinakamataas na halaga ng tugon bago ang pag-abot ng ninanais na halaga) at iba pa(panahong nagpapanatili, pagkabulok na kwarter). Ang mga spesipikasyong sakop na prewkensiya ay karaniwang nauugnay sa malakas na kontrol.

Pagtukoy ng modelo at pagiging malakas

Ang isang sistemang kontrol ay dapat malaking may ilang katangiang pagiging malakas. Ang isang kontroler na malakas ay sa gayong ang mga katangian nito ay hindi labis na nagbabago kung nilalapat sa isang sistema na katamtamang iba mula sa isang matematikal na ginagamit para sa sintesis nito. Ang spesipikasyong ito ay mahalaga. Walang tunay na sistemang pisikal na tunay na umaasal tuldd ng serye ng mga ekwasyong diperensiyal na ginagamit upang ikatawan ito ng matematikal. Sa karaniwan, ang isang mas simpleng modelong matematikal ay pinipili upang pasimplehin ang mga kalkulasyon, kundi ang tunay na dinamika ng ay maaaring labis na komplikado na ang isang kompletong model ay imposible.

Pagtukoy ng sistema

Ang proseso ng pagtukoy ng mga ekwasyong nangangasiwa sa dinamika ng modelo ay tinatawag na pagtukoy ng sistema. Ito ay maaaring gawin ng offline. Halimbawa nito ang pagsasagawa ng isang serye ng mga sukat na pagkukwentahan ng isang tinantiyang modelong matematikal na karaniwang ang punsiyong paglilipat nito o matriks. Ang gayong pagtukoy mula sa awtput gayunpaman ay hindi makapagsasaalang alang ng mga hindi mapagmamasdang dinamika. Minsan, ang modelo ay direktang itinayo na nagsisimula mula sa alam na mga ekwasyong pisikal. Halimbawa, sa kaso ng sistemang damper na masa-spring, alam nating ang $m{\ddot {x}}(t)=-Kx(t)-\mathrm {B} {\dot {x}}(t)$ . Kahit pa ipagpalagay na ang isang kompletong modelo ay ginagamit sa pagdidisenyo ng gayong kontroler, ang lahat ng mga parametrong isinama sa mga ekwasyong ito(na tinatawag na mga parametrong nominal) ay hindi kailanman malalaman nang may absolutong presisyon. Ang sistemang kontrol ay kailangang umasal ng tama kahit na nakakonekta sa isang sistemang pisikal na may mga halagang tunay na parametro na malayo sa nominal. Ang ilang mas mataas na mga pamamaraang kontrol ay kinabibilangan ng isang proseng online ng pagtukoy. Ang mga parametro ng modelo ay kinukwenta(tinutukoy) habang ang mismong kontroler ay tumatakbo. Sa paraang ito, kung ang isang drastikong pagkakaiba ng mga parametro ay nangyari(halimbawa, kung ang braso ng robot ay nagpakawala ng timbang), isasaayos ng kontroler ang sarili nito upang masiguro ang tamang pagganap.

Analisis

Ang analisis ng pagiging malakas ng isang sistemang kontrol na SISO ay maaaring isagawa sa sakop na prekwensiya na nagsasaalang ng punsiyong paglipat ng sistema at gamit ang diagramang Nyquist at diagramang Bode. Ang mga paksa ay kinabibilangan ng marhin na pakinabang at yugto at marhin na amplitudo. Para sa MIMO at sa pangkalahatan, mas komplikadong mga sistemang kontrol, dapat isaalang alang ng isa ang mga resultang teoretikal nilikha para sa bawat pamamaraan ng kontrol: i.e. kung ang partikular na mga kalidad ng pagiging malakas ay kailangan, dapat ilipat ng inhinyero ang kanyang atensiyon sa isang paraang kontrol sa pamamagitan ng pagsasama ng mga ito sa mga katangian nito.

Mga pagtatakda

Ang isang partikular na isyu ng pagiging malakas ang inaatas para sa isang sistemang kontrol na angkop na gumanap sa presensiya ng mga pagtatakdang input at estado. Sa mundong pisikal, ang bawat signal ay nalilimitahan. Maaaring mangyari na ang isang kontroler ay magpapadala ng mga signal ng kontrol na hindi masusundan ng sistemang pisikal. Halimbawa nito ang pagsubok sa pag-iikot ng valve sa isang labis na bilis. Ito ay maaaring lumikha ng hindi kanais nais na pag-aasal ng sistemang saradong loop o makapinsala o sumira sa mga aktuwador o iba pang mga pangilalim na sistema. Ang mga spesipikong pamamaraang kontrol na magagamit upang lutasin ang problema ang kontrol na prediktibong modelo at mga sistemang anti-wind up. Ang huli ay binubuo ng karagdagang blokeng kontrol upang masiguro na ang signal na kontrol ay hindi kailanman lalagpas sa isang ibinigay na threshold.

Mga klasipikasyon ng sistema

Kontrol ng mga sistemang linyar

Para sa mga sistemang MIO, ang paglalagay ng polo ay maaaring isagawa ng matematiko gamit ang representasyong estado espasyo ng sistemang bukas na loop at pagkukwenta ng isang matriks na feedback sa pagtatakda ng mga polo sa mga ninanais na posisyon. Sa mga sistemang komplikado, ito ay mangangailagan ng mga kakayahang pagkukwenta na tinutulungan ng kompyuter at hindi palaging makasisiguro ng pagiging malakas. Sa karagdagan, ang lahat mga estado ng sistema ay hindi pangkalahatang sinusukat at kaya ang mga nagmamasid ay dapat isama sa disenyo ng paglalagay ng polo.

Kontrol ng mga sistemang hindi linyar

Ang mga proseso sa mga industriyang tulad ng robotika at industriyang aeroespasyo ay karaniwang may malakas na dinamikang hindi linyar. Sa teoriya ng kontrol, minsang posible na ilinyar ang gayong mga klase ng sistema at ilapat ang mga pamamaraang linyar ngunit sa maraming mga kaso, maaaring kinakailangang lumikha mula sa simula na pumapayag sa kontrol ng mga sistemang hindi linyar. Ang mga ito, halimbawa ang linyarisasyon ng feedback, backstepping, kontrol na modong dumudulas at kontrol na trahektoryong linyarisasyon ay normal na sumasamantala sa mga resultang batay sa teoriya ni Lyapunov. Ang heometriyang diperensiyal ay malawak na ginagamit bilang kasangkapan sa paglalahat ng mga mahusay na alam na mga konseptong kontrol na linyar sa mga kasong hindi linyar gayundin sa pagpapakita ng hindi mga madedekta na gumagawa ritong mas nakahahamong problema.

Mga sistemang desentralisado

Kapag ang sistema ay kinokontrol ng maraming mga kontroler, ang problema ay ng kontrol na desentralisado. Ang desentralisasyon ay makakatulong sa maraming mga paraan. Halimbawa, ito ay tumutulong sa mga sistemang kontrol na magpatakbo sa isang malaking sakop na heograpikal. Ang mga ahente sa mga sistemang desentralisadong kontrol ay maaaring makipagugnayan gamit ang mga channel ng komunikasyon mag-kokoordina ng kanilang mga aksiyon.

Mga pangunahing stratehiyang kontrol

Ang bawat sistemang kontrol ay dapat gumarantiya muna ng pagiging matatag ng pag-aasal na saradong loop. Para sa mga sistemang linyar, ito ay maaaring makamit sa pamamagitan ng direktang paglalagay ng mga polo. Ang mga sistemang kontrol na hindi linyar ay gumagamit ng mga spesipikong teoriya(normal na batay sa teoriya ni Lyapunov) upang masiguro ang pagiging matatag nang hindi isasaalang alang ang mga panloob na dinamika ng sistema. Ang posibilidad na maisakatuparan ang iba't ibang mga spesipikasyon ay iba iba mula sa modelong isinasaalang alang at sa stratehiyang kontrol na napili. Ang sumusunod ang buod na talaan ng pangunahing mga pamamaraang kontrol:

Adaptibong kontrol: Ang adaptibong kontrol ay gumagamit ng pagtukoy na online ng mga parametro ng proseso o pagbabago ng mga pakinabang ng kontroler at kaya ay nagkakamit ng malakas na mga katangiang pagiging malakas. Ang mga adaptibong kontrol ay inilapat sa unang pagkakatoon sa industriyang aerospace noong mga 1950 at nakahanap ng partikular na tagumpay sa larangang ito.

Hierarkikal na kontrol: Ang isang hierarkikal na kontrol ay isang uri ng sistemang kontrol kung saan ang isang hanay ng mga kasangkapan at nangangasiwang sopwer ay isinaayos sa isang hierarka(puno). Kapag ang mga ugnayan sa puno ay isinagawa ng isang network ng kompyuter, kung gayon ang sistemang kontrol na hierarkikal ay isa ring anyo ng naka network na sistemang kontrol.

Intelihenteng kontrol: Ang intelihenteng kontrol ay gumagamit ng iba't ibang mga pakikitungong pagkukwenta ng Intelihensiyang Artipisyal tulad ng mga network na neural, probabilidad na Bayesian, lohikang fuzzy, pagkatuto ng makina, ebolusyonaryong komputasyon at mga algoritmong henetiko upang kontrolin ang isang sistemang dinamiko.
Optimal na kontrol: Ang optimal na kontrol ay isang partikular na pamamaraang kontrol kung saan ang mga signal ng kontrol ay nagooptimisa ng isang indeks ng gastos. Halimbawa sa kaso ng satellite, ang mga thrust ng jet na kailangan upang dalhin ito sa ninanais na trahektoryong kumokonsumo ng mababang halaga ng petrolyo. Ang dalawang mga pamamaraang disenyong optimal ay malawak na ginagamit sa mga aplikasyong industriyal gaya ng ipinakita na ang mga ito ay gumagarantiya ng pagiging matatag ng saradong loop. Ang mga ito ang kontrol na modelong prediktibo at kontrol na linyar-kwadratiko-Gaussian. Ang una ay hayagang nagsasaalang alang ng mga pagtatakda sa mga signal ng sistema na mahalagang katangian sa maraming mga prosesong indusriyal. Gayunpaman, ang istrakturang optimal na kontrol sa MPC ay isa lamang paraan upang makamit ang gayong resulta dahil hindi ito nag-ooptimisa ng isang tunay na indeks ng pagganap ng sistemang kontrol na saradong loop. Kasama ng mga kontroler na PIC, ang mga sistemang MPC ang pinaka malawak na ginagamit na pamamaraang kontrol sa prosesong kontrol.
Malakas na kontrol: Ang malakas na kontrol ay hayagang umuukol sa kawalang katiyakan sa pakikitungo nito sa disenyo ng kontroler. Ang mga kontroler na dinisenyo gamit ang mga pamamaraang malakas na kontrol ay may kagawiang makaya ang mga maliit na pagkakaiba sa pagitan ng tunay na sistema at modelong nominal na ginagamit para sa disenyo. Ang mga simulang pamamaraang ni Bode at iba ay katamtamang malakas. Ang mga pamamaraang estado espasyong inimbento noong mga 1960 at 1970 ay minsang natagpuang walang kalakasan. Ang isang modernong halimbawa ng pamamaraang malakas na kontrol ang paghuhugis ng H-infinity loop na pinaunlad nina Duncan McFarlane at Keith Glover ng Unibersidad Cambridge, Nagkakaisang Kaharian. Ang mga pamamaraang malakas ay naglalayon na makamit ang pagganap na malakas at/o pagiging matatag sa presensiya ng maliit na mga pagkakamali ng pagmomodelo.

Stokastikong kontrol: Ang stokastikong kontrol ay umuukol sa disenyo ng kontrol na may walang katiyakan sa modelo. Sa tipikal na mga problemang kontrol na stokastiko, pinagpapalagay na may umiiral na randomang ingay at mga pagkaabala sa modelo at kontrol at ang disenyong kontrol ay nagsasaalang alang mga randomang paglilihis na ito.

Mga sanggunian

↑ "trim point". Inarkibo mula sa orihinal noong 2012-02-08. Nakuha noong 2012-08-30.{{cite web}}: CS1 maint: date auto-translated (link)
↑ Donald M Wiberg (1971). State space & linear systems. Schaum's outline series. McGraw Hill. ISBN 0-07-070096-6.{{cite book}}: CS1 maint: date auto-translated (link)

[1] "trim point". Inarkibo mula sa orihinal noong 2012-02-08. Nakuha noong 2012-08-30.{{cite web}}: CS1 maint: date auto-translated (link)

[2] Donald M Wiberg (1971). State space & linear systems. Schaum's outline series. McGraw Hill. ISBN 0-07-070096-6.{{cite book}}: CS1 maint: date auto-translated (link)

[1]

[2]